凸优化的笔记专栏,预计会分为五个部分,分别是:
- 绪论与凸集
- 凸函数
- 凸优化问题
- 对偶
- 算法
参考:
- Stanford《convex optimization》
- 中科大 凌青 凸优化
优化问题
优化问题:从一系列可行解集合中,寻找出最优的元素
优化问题的形式:
$$ \begin{array}{ll} \text{ minimize } & f_0(x) \newline \text { subject to } & f_{i}(x) \leq b_i \end{array} $$
$f_0$是目标函数($R^n \to R$)
优化问题在现实生活中各个领域都非常常见,深度学习中也是要使Loss最小,也是优化问题。
优化问题的分类
线性优化/非线性优化
(有时候也叫规划,和优化是一个意思)
目标函数由多个线性函数组合成,就是线性优化问题,否则就是非线性优化问题。
线性优化问题,最优解不是在顶点就是在整条边上
凸优化/非凸优化
凸优化:
$$ \begin{array}{ll} \text{ minimize } & f_0(x) \newline \text { subject to } & f_{i}(x) \leq 0, \quad i=1, \ldots, m \newline & a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p \end{array} $$
优化问题里面,比较好求解的是凸优化问题,非凸优化问题难解决
光滑/非光滑
目标函数每个点都可微就是光滑的,否则是非光滑的
连续/离散
按照可行域连续或者离散分类
单目标/多目标
对多个目标进行优化
这门课只研究单目标连续光滑的凸优化问题
判断是否为凸问题的一个关键,就是看约束集合、目标函数是否是凸集。所以凸集是凸优化问题最基本的一个概念。
仿射集 Affine set
集合中任取两个点,形成的直线,如果整条线上的点也都在集合中,那么称该集合为仿射集 要求任意两点连成的直线在集合中,也就是说
$$x_1, x_2 \in C, \theta\in R \to \theta x_1 + (1- \theta)x_2 \in C$$

仿射组合:不仅限两个点,而是多个点: $$x_1,...x_k \in C , \theta_1 + ... \theta_k = 1 \to \theta_1 x_1 + ... \theta_k x_k \in C$$
利用 $$ (\theta_1 + \theta_2)(\frac{\theta_1}{\theta_1 + \theta_2}x_1 + \frac{\theta_2}{\theta_1 + \theta_2}x_2) + (1-\theta_1 - \theta_2)x_3 \in C $$即可证明
任意线性方程组$Ax = b$的解集都是仿射集,任意仿射集都可以写成线性方程组的解集
假设该线性方程组有两个解$x_1, x_2$,则直线上的任意一点$\theta x_1+(1-\theta)x_2$代入得$A(\theta x_1+(1-\theta)x_2) = b$,说明也是该线性方程组的解
仿射包:从非仿射集合中构造一个最小的仿射集
比如两个点的集合不是仿射集,构造一个经过它们的直线,就是仿射集了,这条直线就是仿射包。三个不同直线的点,它们的最小的仿射包就是经过它们的二维平面。如果本身就是仿射集,那么仿射包就是它自己。
凸集 convex set
凸集相比于仿射集条件放松,要求任意两点连成的线段在集合中。凸集的定义为:
$$x_1, x_2 \in C, \theta\in[0,1] \to \theta x_1 + (1- \theta_2)x_2 \in C$$
仿射集必然是凸集,可以认为是一种特殊的凸集,凸集包含的更广。
凸组合:不仅限两个点,而是多个点: $$x_1,...x_k \in C , \theta_1 + ... \theta_k = 1, \theta_i\in[0,1] \to \theta_1 x_1 + ... \theta_k x_k \in C$$
凸包:包含集合S的最小凸集
下图2.2,只有左边的凸多边形是凸集。不过如果右图只少了角点,是凸集,少了边上或者内部的点就不是凸集了。
下图2.3是凸包,包括一组离散点的凸包,以及非凸形状的凸包。
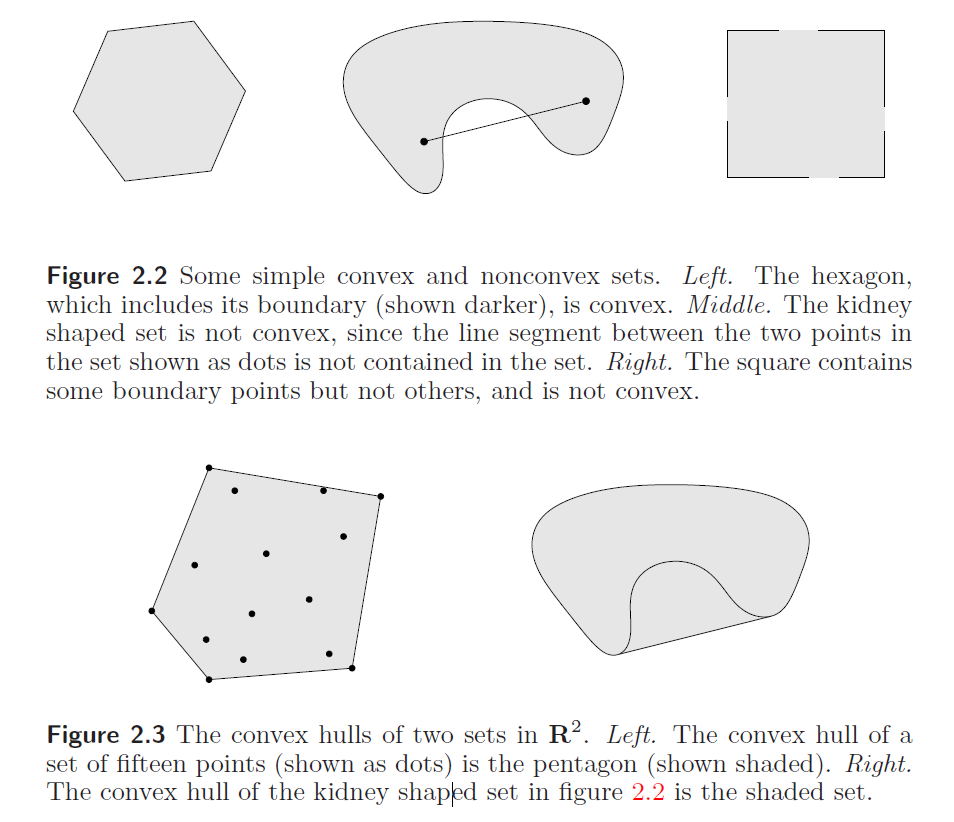
典型凸集
凸锥 Convex cone
锥:$\forall x \in C, \theta \geq 0, \theta x \in C$(锥尖需要在原点)
凸锥:$x_1, x_2 \in C, \theta_1 x_1 + \theta_2 x_2 \in C, \theta_1 > 0, \theta_2 > 0$
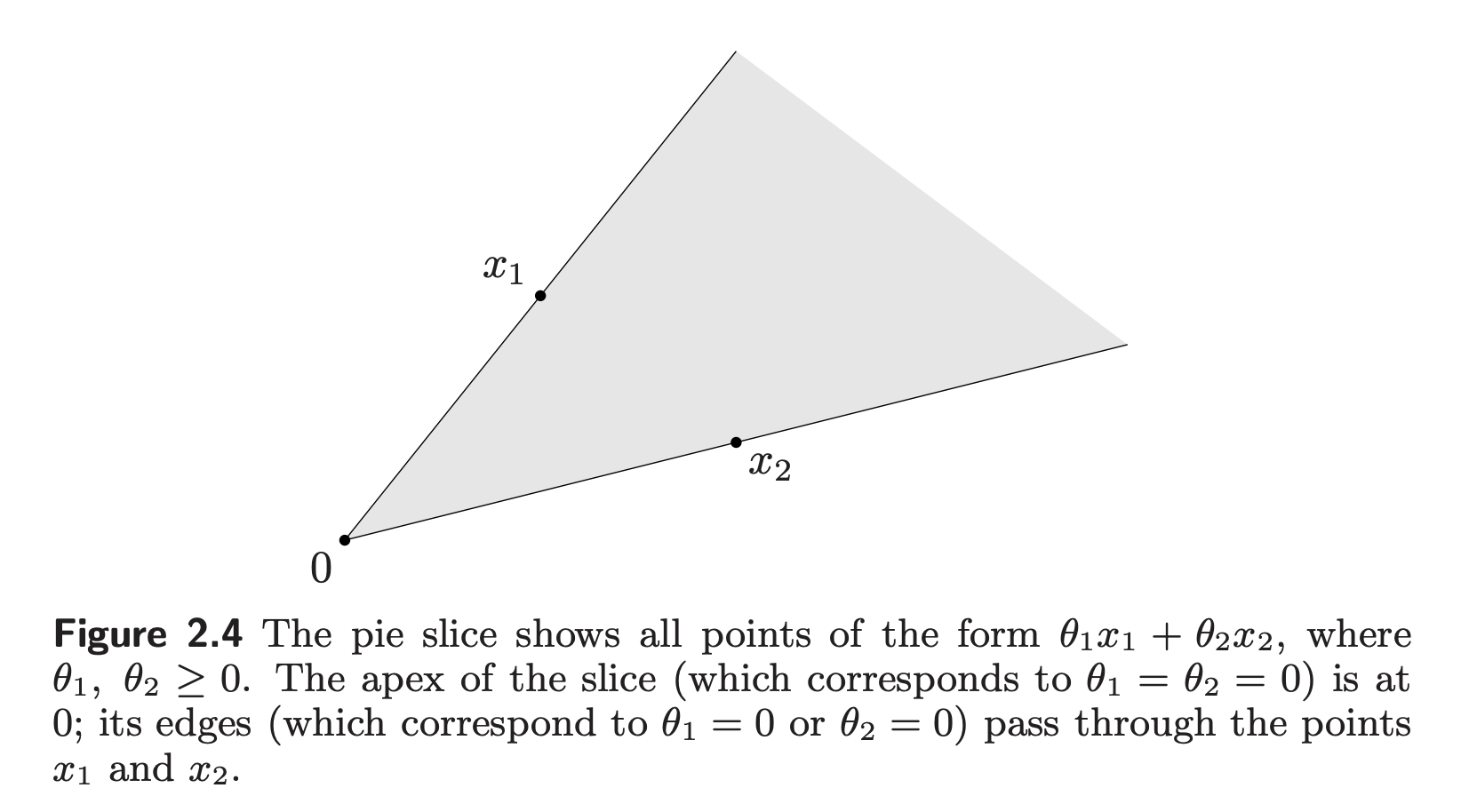
图形理解,任取两点$x_1, x_2$,如果$x_1,x_2,o$不在一条直线上,那么在$\overset{\frown}{x_1 o x_2}$的扇形区域内的所有的点都在凸锥集上
过原点的直线和原点发出的射线是凸锥
凸锥组合:$x_1,... x_k \in C, \theta_1 x_1 + ... \theta_k x_k \in C, \theta_1 > 0, ... \theta_k > 0$
凸锥包:和前面一样,如下图所示
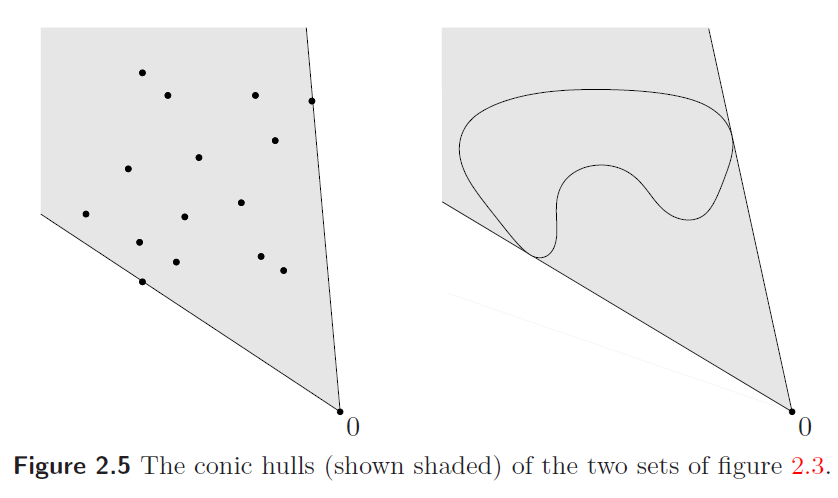
对比一下前面几种组合: 仿射组合:$\theta_1 + ... + \theta_k = 1$ 凸组合:$\theta_1 + ... + \theta_k = 1, \theta_1, ... , \theta_k > 0$ 凸锥组合:$\theta_1, ... , \theta_k \geq 0$
超平面 Hyperplane
${x|a^T x = b}$
是仿射集,也是凸集,不一定凸锥(除非过原点)
半空间 Halfspace
${ x|a^T x \leq b }$
半空间是凸集,不是仿射集,不一定凸锥(除非过原点)
下图分别为超平面和半空间:

证明: 假设$x_1, x_2$在空间上: $a^T x_1 \leq b$ $a^T x_2 \leq b$ 对于$x_1,x_2$上的任意一点$\theta x_1 + (1-\theta) x_2$有: $a^T(\theta x_1 + (1-\theta) x_2) = \theta (a^T x_1 -b) + (1-\theta) (a^T x_2 - b) +b \leq b$,也在集合中,所以半空间是凸集
法线的反方向
空间球 Euclidean Ball
欧几里得球,就是一个空间球
$$ B\left(x_{c}, r\right)=\newline{x |\ ||x-x_{c}||_2\leq r \newline} $$
$$=\newline{x |\ (x-x_{c})^{T}(x-x_{c} ) \leq r^2\newline} $$
证明: 假设$x_1, x_2$在空间上: $|| x_1 - x_c ||_2 \leq r$ $|| x_2 - x_c ||_2 \leq r$ 对于$x_1,x_2$上的任意一点$\theta x_1 + (1-\theta) x_2 $,(其中$\theta \in [0,1]$),有: $$|| \theta x_1 + (1-\theta) x_2 - x_c ||_r = || \theta (x_1 - x_c) + (1-\theta)(x_2 - x_c)||\newline \leq \theta ||x_1 - x_c||_2 + (1-\theta) ||x_2 - x_c||_2 \leq r $$ 这里用到了范数的三角不等式
范数性质 假设$x$的范数是$f(x)$,$f(x)\geq 0$,满足下面三条性质: $\text{if}\ f(x)=0 \to x=0$ $kf(x) = |k|f(x)$ $f(x+y) \leq f(x) + f(y)$(三角不等式)
椭球 Ellipsoids
$$\mathcal{E} = \{ x \mid\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leq 1 \}$$
矩阵P是一个 $n\times n$ 的对称正定矩阵
(特征值,奇异值)
多面体 Polyhedra
多面体:有限个线性等式和不等式的解集 多面体是有限个半空间和超平面的交集
$$ \mathcal{P}=\newline{x \mid a_{j}^{T} x \leq b_{j}, j=1, \ldots, m, c_{j}^{T} x=d_{j}, j=1, \ldots, p\newline} $$
范数球 Norm Ball & 范数锥 Norm Cone
范数:满足以下条件的函数$||\cdot||$ 1、$||x||\geq 0$,$||x||=0$当且仅当$x=0$ 2、$||tx|| = t||x||$,对于任何$t\in R$成立 3、$||x+y|| \leq ||x|| + ||y||$
$$ C={(x, t) \mid|x| \leq t} \subseteq \mathbf{R}^{n+1} $$
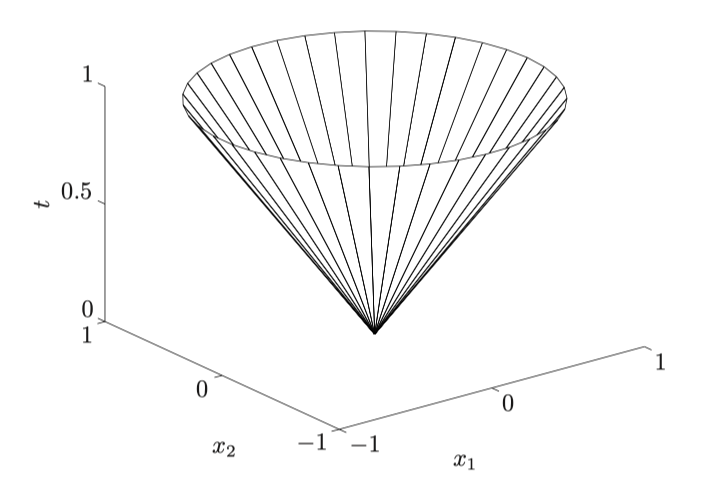
其他的例子
n*n的对称矩阵组成的集合,是凸锥,也是凸集
n*n的半正定矩阵组成的集合,是凸集
n*n的正定矩阵组成的集合不是凸集(取值只能>=0,不属于正定了)
线性矩阵不等式的解集也是凸集
保凸运算
如果要证明是凸集可以用定义法,不过复杂情况会很难证明。 另一种方法是证明集合是多个凸集的保凸运算的简单组合,保凸运算包括以下几个:
交集 Intersection
$C_1$, $C_2$是凸集,其交集$C = C_1 \cap C_2$也一定是凸集。
拓展到n个也是。
仿射函数 Affine
$f$是仿射变换:$\mathbf{R}^{n} \rightarrow \mathbf{R}^{m}$
如果有$S \in R^n$是凸集,那么$f(S)=\newline{f(x) \mid x \in S\newline}$也是凸集,用定义证明即可。 逆函数$f^{-1}(S)=\newline{x \mid f(x) \in S\newline}$也是凸集。
透视函数 Perspective functions
透视函数 $P: \mathbf{R}^{n+1} \rightarrow \mathbf{R}^{n}$,相当于通过变换(所有元素除以最后一个元素)将最后一个维度的元素变为1,然后去掉这个维度的一种变换。降低一个维度。
$P(\mathbf{X}, t) = \mathbf{X}/t, dom P = \newline{(\mathbf{X}, t), t > 0\newline}$ 这里t是一个标量,X是矩阵,相当于P是dom(X)+1维度的,去掉最后一个维度t,X里的每一个元素除以t。
类比于针孔相机,3维的点$(x_1, x_2, x_3)$会通过孔映射到二维的平面 $-(x_1/x_3, x_2/x_3, 1)$ 上,就是一个透视函数的过程。
任意凸集的反透视映射也是凸集
线性分段函数 Linear-fractional
一个Linear-fractional function是由perspective function和一个affine function组成的
$g(x)=\left[\begin{array}{c}A \newline c^{T}\end{array}\right] x+\left[\begin{array}{l}b \newline d\end{array}\right]$
超平面分离定理与支撑超平面
超平面分离定理
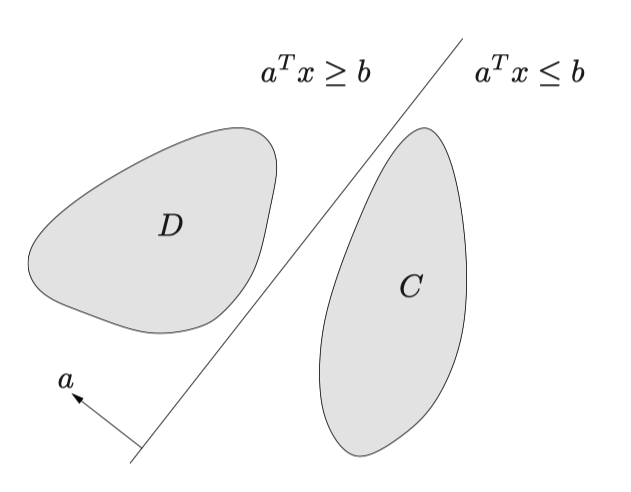
如果$C$和$D$是两个不相交的凸集,那么必然存在一个超平面$\newline{x|a^Tx = b\newline}$能够分离$C$和$D$,这超平面被称为分割超平面
支撑超平面
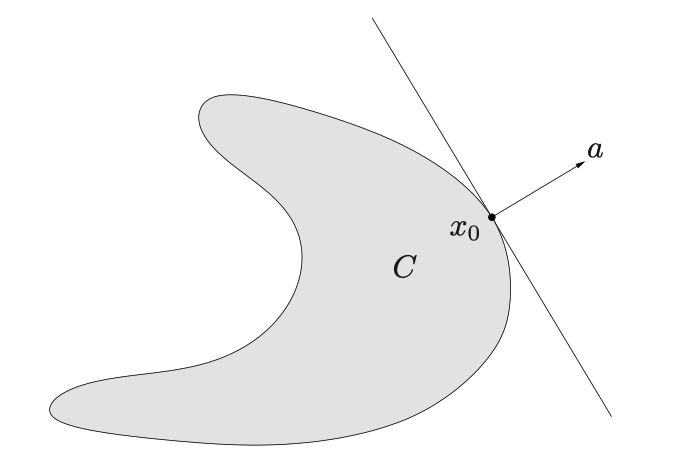
集合C边界上的点$x_0$的支撑超平面:$\newline{x | a^Tx = a^T x_0\newline}$
其中$a \neq 0$,对于所有的$x \in C$满足$a^Tx \leq a^T x_0$
如果$C$是凸的,那么C边界上的每一个点都存在一个支撑超平面。
例题
设$C \subseteq R^n$是一个凸集,证明对于任意$k$的情况,满足$\theta_i \geq 0, \theta_1 + ... \theta_k = 1$的情况下,有$\theta_1 x_1 + ... + \theta_k x_k \in C$。
证明:使用数学归纳法, $k=2$时,根据凸集的定义性质可知,任取$\theta_1, \theta_2$,满足$\theta_1+\theta_2=1$,有$\theta_1 x_1 + \theta_2 x_2 \in C$
假设$k=n-1$时上式成立,即满足$\theta_1+ ... +\theta_{n-1}=1$,有$\theta_1 x_1 + ... + \theta_{n-1} x_{n-1} \in C$
下面考虑$k=n$的情况,构造下面的式子:
$$ (\sum_{i=1}^{k-1} \theta_i) \frac{\sum_{i=1}^{k-1} \theta_i x_i}{\sum_{i=1}^{k-1}\theta_i} + (1-\sum_{i=1}^{k-1} \theta_i)x_i $$
其中$\frac{\sum_{i=1}^{k-1} \theta_i x_i}{\sum_{i=1}^{k-1}\theta_i}$完全符合$n-1$的条件,所以$\frac{\sum_{i=1}^{k-1} \theta_i x_i}{\sum_{i=1}^{k-1}\theta_i} \in C$,整个式子又满足$k=2$的凸集的定义,所以有: $$ (\sum_{i=1}^{k-1} \theta_i) \frac{\sum_{i=1}^{k-1} \theta_i x_i}{\sum_{i=1}^{k-1}\theta_i} + (1-\sum_{i=1}^{k-1} \theta_i)x_i \in C $$
即证明了只要$k=n-1$时成立,就有$k=n$时成立,数学归纳法得证
判断下面的哪些集合是凸集
(a)平板,形如$\newline{x \in \mathbf{R}^{n} \mid \alpha \leqslant a^{T} x \leqslant \beta\newline}\newline$
(b)矩形,形如$\newline{x \in \mathbf{R}^{n} \mid \alpha_i \leqslant x_i \leqslant \beta_i\ , i = 1, ..., n \newline}$
(c)楔形,形如$\newline{x \in \mathbf{R}^{n} \mid \alpha_1^T x \leqslant b_1 , \alpha_2^T x \leqslant b_2, i = 1, ..., n \newline}$
(d)距离给定点比距离给定集合近的点构成的集合: $ \newline{ x \mid ||x-x_0||_2 \leq ||x-y||_2, \forall y \in S \newline}$
(e)距离一个集合比另一个集合更近的点的集合:$\newline{x \mid \operatorname{dist}(x, S) \leqslant \operatorname{dist}(x, T)\newline}$
(f)集合$\newline{x \mid x + S_2 \subseteq S_1 \newline}$,其中$S_1, S_2 \subseteq R^n$,并且$S_1$是凸集
(g)到 $a$ 的距离与到 $b$ 的距离之比不超过到某一固定分数$\theta$的点的集合,即集合$\newline{x \mid|x-a|_2 \leqslant \theta |x-b|_2\newline}$
(a)
- 用定义证明:
任取$x_1, x_2 \in C$,有$\alpha \leqslant a^{T} x_1 \leqslant \beta, \alpha \leqslant a^{T} x_2 \leqslant \beta$
对于$\theta \in [0, 1]$,对于$ (\theta x_1 + (1-\theta) x_2)$,有: $$\alpha = \theta \alpha + (1-\theta) \alpha \leq \alpha^T (\theta x_1 + (1-\theta) x_2) \leq \theta \beta + (1-\theta) \beta = \beta$$
即$ (\theta x_1 + (1-\theta) x_2) \in C$,是凸集
- 用保凸性证明:
因为平板是两个半空间的交集,半空间是凸集,交集是保凸运算,所以平板也是凸集
(b)
- 用定义证明:
任取$x_1, x_2 \in C$,有$\alpha_i \leqslant x_1 \leqslant \beta_i, \alpha_i \leqslant x_2 \leqslant \beta_i$
对于$\theta \in [0, 1]$,对于$ (\theta x_1 + (1-\theta) x_2)$,有: $$\alpha_i \leq (\theta x_1 + (1-\theta) x_2) \leq \beta_i$$
即$ (\theta x_1 + (1-\theta) x_2) \in C$,是凸集
- 用保凸性证明:
矩形是多个半空间的交集,半空间是凸集,交集是保凸运算,所以矩形也是凸集
(c)
- 用定义证明:
任取$x_1, x_2 \in C$,有$a_1^{T} x_1 \leqslant b_1, a_2^{T} x_1 \leqslant b_2$、$a_1^{T} x_2 \leqslant b_1, a_2^{T} x_2 \leqslant b_2$
对于$\theta \in [0, 1]$,对于$ (\theta x_1 + (1-\theta) x_2)$,有: $$a_1^T (\theta x_1 + (1-\theta) x_2) \leq \theta b_1 + (1-\theta) b_1 = b_1\newline a_2^T (\theta x_1 + (1-\theta) x_2) \leq \theta b_2 + (1-\theta) b_2 = b_2$$
- 用保凸性证明:
楔形是多个半空间的交集,半空间是凸集,交集是保凸运算,所以楔形也是凸集
(d) 对于固定的$y$而言,有: $$ \begin{array}{ll} &||x-x_0||_2 \leqslant ||x-y||_2\newline \Leftrightarrow & (x-x_0)^T(x-x_0) \leqslant (x-y)^T (x-y)\newline \Leftrightarrow & x^T x - 2x_0^T x + x_0^T x_0 \leqslant x^T x - 2y^T x + y^T y\newline \Leftrightarrow & 2(y^T - x_0^T)x \leqslant y^T y - x_0^T x_0 \newline \end{array} $$ s 说明该集合是多个半空间的交集,交集为保凸运算,所以该集合为凸集
(e) 不是凸集,可以举反例,比如$S = {(x, y)|x^2 + y^2 = 1}$,$T = {(0, 0)}$,那么这个集合就是$R^2$平面挖空一个圆心在原点,半径为$\frac{1}2$的孔,比如集合上取$(0, 1),(0, -1)$两点,取$\theta=0.5$,$(0,0)$不在这个集合内,很显然它不是凸集。
(f) 令$y \in S_2$,集合相当于是多个凸集$(S_1 - y)$的交集,交集为保凸运算,所以也是凸集。
(g) 是凸集 $$ \begin{array}{ll} & ||x-a||_2 \leqslant \theta||x-b||_2\newline \Leftrightarrow & (1-\theta^2)x^Tx - 2 (a-\theta^2b)^Tx + (a^Ta - \theta^2b^Tb) \leq 0 \end{array} $$
如果$\theta \leq 1$,集合是一个球 如果$\theta = 1$,集合是半空间 都是凸集
一些概率分布集合,令$x$为服从分布 $\textbf{prob}(x=a_i) = p_1, i = 1, ... ,n$ 的实数随机变量,$p \in R^n$在一个标准概率单纯形$P=\{p \mid \mathbf{1}^{T} p=1, p \succeq 0\}$,下面哪些条件在$p$中是凸的?
(a)$\alpha \leqslant \textbf{E} f(x) \leqslant \beta$
(b)$\textbf{prob}(x>\alpha) \leqslant \beta$
(c)$\textbf{E} |x^3| \leqslant \alpha \textbf{E} |x|$
(d)$\textbf{E} x^2 \leqslant \alpha$
(e)$\textbf{E} x^2 \geqslant \alpha$
(f)$\textbf{var} (x) \leqslant \alpha$
(g)$\textbf{var} (x) \geqslant \alpha$
(h)$\textbf{quartile} (x) \geqslant \alpha$,$\textbf{quartile} (x) = \text{inf} \{ \beta | \textbf{prob}(x\leqslant \beta) \geqslant 0.25\}$
(i)$\textbf{quartile} (x) \leqslant \alpha$
$p$的约束:$p_i \geq 0$是n个半空间,约束$\sum_{i=1}^n = 1$是超平面,也就是说$p$是一个多面体,本身为凸集。
(a) $\alpha \leq \sum_{i=1}^n p_i f(a_i) \leq \beta$ 增加线性不等式约束,仍为凸集
(b) $\textbf{prob}(x\geq \alpha) = \sum_{i, a_i \geq \alpha}p_i \leq \beta$ 增加线性不等式约束,仍为凸集
(c) $\mathbf{E}\left|x^{3}\right| \leq \alpha \mathbf{E}|x| \to \sum_{i=1}^{n} p_{i}\left(\left|a_{i}^{3}\right|-\alpha\left|a_{i}\right|\right) \leq 0$ 增加线性不等式约束,仍为凸集
(d) $\sum_{i=1}^{n} p_{i} a_{i}^2 \leq \alpha$ 增加线性不等式约束,仍为凸集
(e) $\sum_{i=1}^{n} p_{i} a_{i}^2 \geq \alpha$ 增加线性不等式约束,仍为凸集
(f) $\textbf{var}(x)=\mathbf{E} x^2-(\mathbf{E} x)^2=\sum_{i=1}^{n} p_{i} a_{i}^2-\left(\sum_{i=1}^{n} p_{i} a_{i}\right)^2 \leq \alpha$ 不是凸集。举反例,比如$a_1 = 0, a_2 = 1, \alpha = 0.2$,两个点$p_1 = (0, 1), p_2 = (1,0)$,有$\textbf{var}(x) \leq \alpha$,但是中间的点$(\frac{1}2, \frac{1}2)$明显不满足。
(g) $\textbf{var}(x)=\mathbf{E} x^2-(\mathbf{E} x)^2=\sum_{i=1}^{n} p_{i} a_{i}^2-\left(\sum_{i=1}^{n} p_{i} a_{i}\right)^2 = b^T p + p^T A p \geq \alpha$ 因为$A = a a^T$是半正定的,所以是凸集
(h) $\textbf{prob}\left(x \leq a_{k}\right)=\sum_{i=1}^{k} p_{i}<0.25$ 是一个半空间,是凸集。
(i) $\sum_{i=k+1}^{n} p_{i} \geq 0.25$ 是一个半空间,是凸集。