背景与简介
在生物医学、金融保险等领域,生存分析是一种很常见而且重要的方法。
生存分析主要用在癌症等疾病的研究中,比如对某种抗癌药物做临床试验,筛选一部分癌症患者,分为两组,一组服用该试验药物,一组服用对照药物,服药后开始统计每个患者从服药一直到死亡的生存时间。
生存分析可以抽象概述为,研究在不同条件下,特定事件发生与时间的关系是否存在差异。这些具体事件可以是死亡,也可以是痊愈、肿瘤转移、复发、出院、重新入院等任何可以明确识别的事件,而不同条件即为不同的分组依据,可以是年龄、性别、地域、某个基因表达量的高低、某个突变的携带与否等等。
(后面均用"死亡"来代指这个特定事件
概念与推导
生存时间T
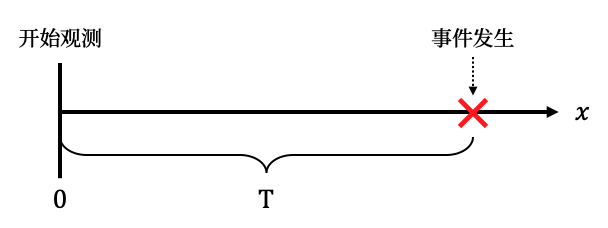
把生存时间作为一个随机变量,用PDF(概率密度函数)和CDF(分布函数)来表达
其中CDF为$F(t) = Pr(T < t)$,也就是t之前死亡的概率
生存概率
S(t),Survival probability,研究对象从试验开始到某个特定时间点仍然存活的概率,$S(t) = pr(T > t)$
$S(t) = 1 - F(t)$
之后的Kaplan-Meier模型主要关注S(t)
风险概率
$h(t): \text{Hazard function}$
$$h(t) = \lim_{\epsilon \to 0}\frac{P(T \in (t, t+\epsilon] | T \geqslant t)}{\epsilon} = \frac{f(t)}{S(t)}$$
前一个等号的意义 很明显,表示的意义就是研究对象从试验开始到某个特定时间点t之前存活,但是在t时间点发生"死亡"的概率
后面一个等号的推导过程
$$ \begin{array}{llr} h(t)& = \lim_{\Delta t \to 0} \frac{P(t < T \leqslant t + \Delta t | T > t)}{\Delta t}\newline & = \lim_{\Delta t \to 0} \frac{P(t < T \leqslant t + \Delta t )}{\Delta t S(t)} & \scriptsize{S(t)的定义}\newline & = \lim_{\Delta t \to 0} \frac{F(t + \Delta t) - F(t)}{\Delta t S(t)} & \scriptsize{F(t)的定义}\newline & = \frac{f(t)}{S(t)}& \scriptsize{f(t)是F(t)的微分} \end{array} $$
然后还可以进一步推导:
$$ h(t) = \frac{f(t)}{S(t)} = \frac{f(t)}{1 - F(t)} = - \frac{\partial log[1 - F(t)]}{\partial t} = - \frac{\partial log[S(t)]}{\partial t} $$
表示了$h(t)$和$S(t)$的关系
$H(t): \text{Comulative\ Hazard\ function}$ $$H(t) = \int_0^t h(u) du$$
进一步推导: $$H(t) = \int_0^t h(u) du = - \int_0^t \frac{ \partial log[S(u)]}{\partial u} du = -log[S(t)]$$
$$\to S(t) = exp[-H(t)]$$
之后的Cox比例风险模型主要关注H(t)
Hazard function理解
hazard function 本身不是概率,它描述的是一种在给定时间点的风险,$\Delta t \times h(t)$表示在$(t, t + \Delta t]$的概率
hazard function优势:
- 描述给定时间点的风险,这是我们需要的信息
- 可以很好的处理数据缺失的情况
举个例子
假设survival time服从指数分布$Exp(\lambda)$,即$f(x) = \lambda e ^{-\lambda x}, x > 0$
也就是$f(t) = \lambda e ^{-\lambda x}$
可以推出:
$F(t) = 1 - e ^{-\lambda x}$
$S(t) = 1 - F(t) = e ^{-\lambda x}$
$h(t) = \frac{f(t)}{S(t)} = \lambda$
$H(t) = \lambda t$
$E(T) = \frac{1}{\lambda} (指数分布的性质)= \frac{1}{h(t)}$
其他的分布同理 Gamma distribution Weibull distribution Log-normal distribution generized gamma distribution...
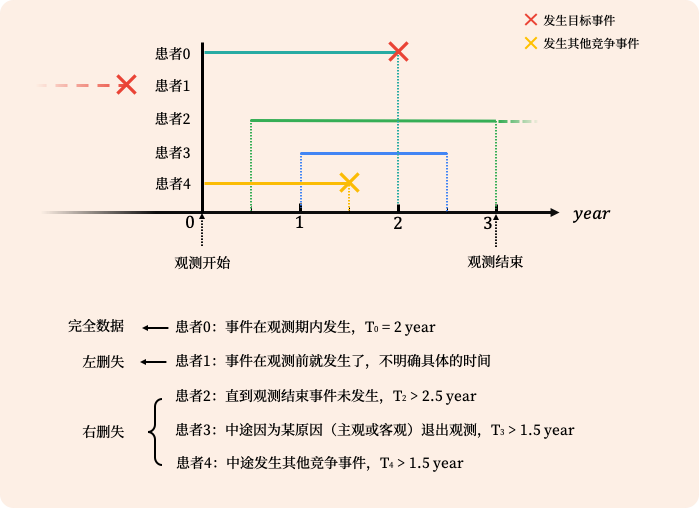
删失数据 Censoring
生存分析中,很常见的一种特征就是删失数据
指的是在临床试验中,出现一些数据丢失的情况,比如病人中途主动退出、无法联系到、结束时还未发生特定事件。保留了从一开始到丢失前进度的数据成为右删失,另一种称为左删失。(后面只讨论右删失)
Type I Censoring:观测时间确定
每一项数据增加一个表示:
$$(U_i, \delta_i) = {min (T_i, c), I(T_i \leqslant c)}, i = 1, ... , n$$
$$I(T_i \leqslant C) = \begin{cases} 1, & T_i \leqslant C,\ 0, & T_i > C \end{cases}$$
c是实验时间,是一个常量 也就是说如果是$(c, 0)$,则代表被删失,如果是$(T_i, 1)$,则没有被删失
Type II Censoring:观测人数确定
比如观测n人,当死亡r人时停止试验 $T_{(1, n)}, T_{(2, n)}, ..., T_{(r, n)}$
Type III Censoring:随机Censoring
不用常量c而是用随机变量$C_i$
$(U_i, \delta_i) = {min (T_i, C_i), I(T_i \leqslant C_i)}, i = 1, ... , n$
只考虑右删失,我们只观察$(U_i, \delta_i)$ 如果$(U_i, \delta_i) = (u_i, 1)$,则说明$T_i = u_i, C_i > u_i$ 如果$(U_i, \delta_i) = (u_i, 0)$,则说明$T_i \geqslant u_i, C_i = u_i$
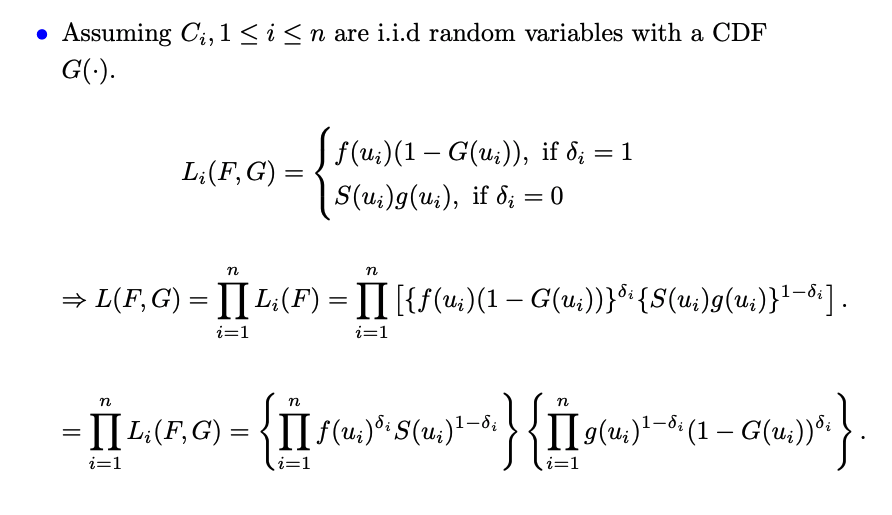
(推导见https://www.bilibili.com/video/BV1WE411P78Z?p=2)
Kaplan-Meier模型
与生存表、Cox并列的一种生存分析的方法,也叫乘积极限(product-limit estimator)
$\hat{S}(t)=\prod_{i: t_{i} \leq t}\left(1-\frac{d_{i}}{n_{i}}\right), \quad t \geq 0$
$d_i$是在$t_i$时刻死亡的人数,$n_i$是还在风险中的人数
例子:
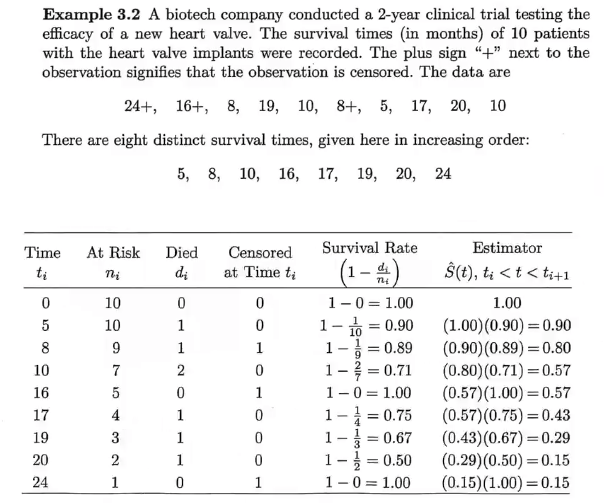
Life table 生存表
举例:
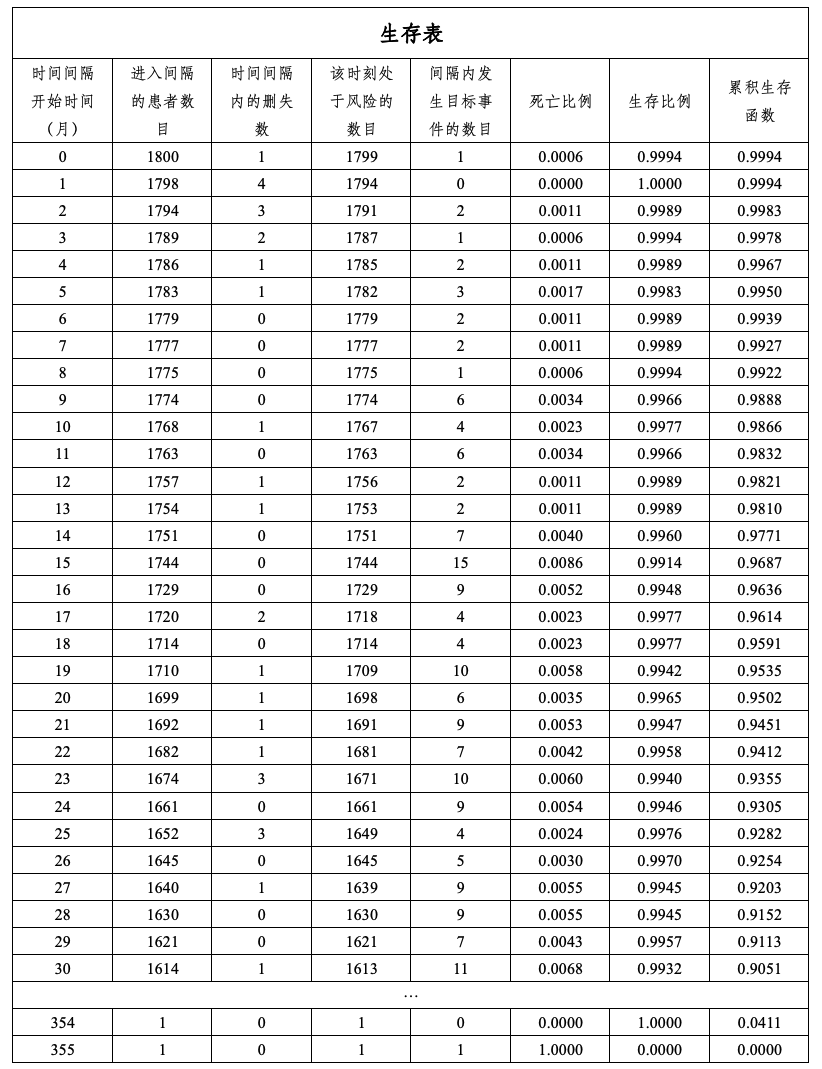
设时间点为$t_0, t_1, ... ,t_n$,那么在$t_i$时间点下的生存概率: $$S(t_i) = \Pi_{j=0}^{i}(1-P(t_j死亡))$$
也就是: $$S\left(t_{i}\right)=S\left(t_{i-1}\right)\left(1-\frac{d_{i}}{n_{i}}\right)$$
$n_i$表示$t_i$时的有效人数,$d_i$表示$t_i$时的死亡人数
$t_i$处的生存率等于$t_{i-1}$时的生存率乘以(1-$t_i$时间点的死亡率)
Kaplan-Meier 生存曲线:
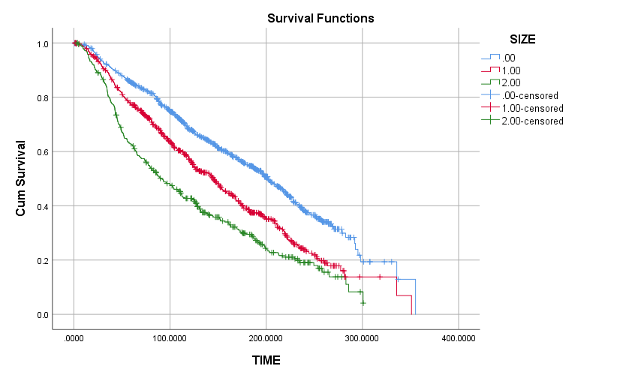 加号表示删失数据
加号表示删失数据
往往是多条线(因为是不同的组)
Cox比例风险回归模型
Cox Proportional-Hazards Model是由英国统计学家D.R.Cox于1972年提出的一种半参数回归模型(半参数值既包含参数模型,又包含非参数模型)
参数模型:有限维度,有限个参数就可以表示模型分布,比如正态分布的均值和标准差 非参数模型:属于某个无限维的空间,无法用有限个参数来表示,比如决策树、随机森林
Cox建立回归的是前面提到的$h(x)$ Cox模型: $$h(t) = h_0(t) \times exp({b_1x_1 + b_2x_2 + ... b_px_p})$$
其中$h(t)$指的是不同时间的风险值(hazard),$x_i$指的是具有预测效应的变量,$b_i$指的是每个变量对应的效应值,$h_0(t)$是基准风险函数,根据不同的数据来使用不同的分布模型,是非参数模型
建模时,首先确定需要研究的可能影响生存率的因素,也就是$x_i$,我们主要要做的就是找到合适的$h_0(t)$以及所有协变量的系数$b_p$,需要用到极大似然估计等方法求解参数。
两个基本假设
对公式两边取对数进行变形:
$$log(h(t)) = log(h_0(t)) + \beta X$$
- 模型中各危险因素对危险率的影响不随时间改变,且与时间无关
- 对数危险率与各个危险因素呈线性相关
参数的极大似然估计
通过极大似然估计来求解参数,极大似然估计的思想是,让已经发生的事件出现的可能性最大。
举个例子,有三个人$X_1, X_2, X_3$分别在三个时间点$t_1, t_2, t_3$死亡
以$t=t_1$为例,此时我们的目标是$max\ h(t_1, X_1)$和$min\ h(t_1, X_2) + h(t_1, X_3)$,统一这两个的目标:
$$max\ \frac{h(t_1, X_1)}{h(t_1, X_1) + h(t_1, X_2) + h(t_1, X_3)}$$
(分母加一个分子不影响结果,但是可以让最后一项不至于分母为0)
类推得到$t_2$的目标: $$max\ \frac{h(t_2, X_2)}{h(t_2, X_2) + h(t_2, X_3)}$$
$t_3$的目标: $$max\ \frac{h(t_3, X_3)}{h(t_3, X_3)}$$
所以似然函数是: $$L(\beta) = \frac{h(t_1, X_1)}{h(t_1, X_1) + h(t_1, X_2) + h(t_1, X_3)} \frac{h(t_2, X_2)}{h(t_2, X_2) + h(t_2, X_3)} \frac{h(t_3, X_3)}{h(t_3, X_3)}$$
代入$h(x)$的公式之后消掉$h_0(t)$,得到: $$L(\beta) = \frac{exp(\beta · X_1)}{exp(\beta · X_1) + exp(\beta · X_2) + exp(\beta · X_3)} \frac{exp(\beta · X_2)}{exp(\beta · X_2) + exp(\beta · X_3)} \frac{exp(\beta · X_3)}{exp(\beta · X_3)}$$
这里我们假设的是3个事件,再泛化到N个的情况: $$L(\beta)=\prod_{i=1}^{N} \frac{\exp \left(\beta \cdot X_{i}\right)}{\sum_{j: t_{j} \geq t_{i}} \exp \left(\beta \cdot X_{j}\right)}$$
对数似然函数: $$l(\beta)=\log L(\beta)=\sum_{i=1}^{N}\left[\beta \cdot X_{i}-\log \left(\sum_{j: t_{j} \geq t_{i}} \exp \left(\beta \cdot X_{j}\right)\right)\right]$$
梯度为: $$\frac{\partial l(\beta)}{\partial \beta}=\sum_{i=1}^{N}\left[\beta-\frac{\sum_{j: t_{j} \geq t_{i}} X_{j} \cdot \exp \left(\beta \cdot X_{j}\right)}{\sum_{j: t_{j} \geq t_{i}} \exp \left(\beta \cdot X_{j}\right)}\right]$$
就可以采用梯度下降法来对参数进行估计
解读结果
解得了合适的$h_0(t)$以及协变量系数之后,我们可以比较某个协变量$x_i$在不同值的时候对应的不同风险比$\frac{x_i + 1}{x_i}$。
$$hazard\ ratio = \frac{h_0(t) \times e^{b_1x_1 + b_2x_2 + ...b_i(x_i+1) + ... b_px_p}}{h_0(t) \times e^{b_1x_1 + b_2x_2 + ...b_ix_i + ... b_px_p}} = e^{b_i}$$
举个例子,假如某个指标$x_i$表示年龄,那么对于年龄x和年龄x+1的人来说,死亡风险比是$e^{b_i}$,如果$b_i>0$,则年龄增大,死亡风险增大。反之减小。等于0则是不起作用